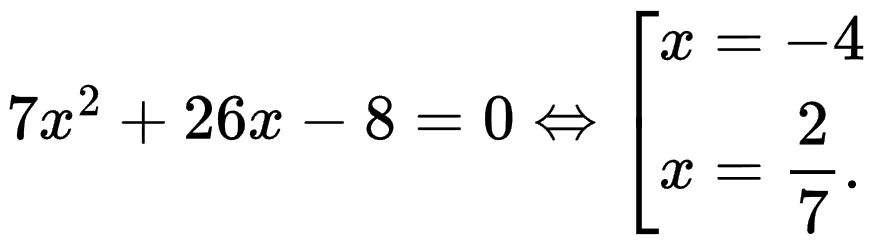
Tạo phương trình bậc hai ngẫu nhiên đơn giản bằng Javascript

Phương trình bậc hai là một trong những kiến thức cơ bản và rất thông dụng trong chương trình Toán phổ thông. Gần đây, nhiều thầy cô đang có khuynh hướng nghiên cứu các thuật toán tạo câu hỏi ngẫu nhiên trong môn Toán, bao gồm cả phương trình bậc hai. Thật ra, ngôn ngữ lập trình nào cũng làm được điều này. Tuy cú pháp mỗi ngôn ngữ có khác nhau, nhưng giải thuật thì không đổi. Javascript có thể chạy trực tiếp trên web mà không cần cài đặt, lại còn hỗ trợ render công thức toán học rất trực quan. Tuy không thể xuất file như PHP hay Python nhưng cũng đáp ứng được rất nhiều yêu cầu khác. Nào, bắt đầu thôi!

Ý tưởng

Yêu cầu hôm nay là viế chương trình tạo phương trình bậc hai có hai nghiệm $x_1=\dfrac{a}{b}$ và $x_2=\dfrac{c}{d}$.

Áp dụng định lý Vi-et, ta có phương trình $x^2-\left(\dfrac{a}{b}+\dfrac{c}{d}\right)x+\dfrac{a}{b}\cdot\dfrac{c}{d}=0$ hay $bdx^2-(ad+bc)x+ac=0$.

Vậy ra, chỉ cần random bốn biến $a$, $b$, $c$, $d$ là có được phương trình bậc hai theo yêu cầu rồi! Nào có đơn giản như vậy. Bây giờ có mấy vấn đề phát sinh như sau:

  1. Javascript không có sẳn lệnh random tạo số nguyên ngẫu nhiên trong khoảng cho trước, tức là mình phải tự xây dựng hàm.
  2. Nếu phương trình bậc hai được tạo thành vẫn chưa được rút gọn các hệ số thì vẫn chưa đạt yêu cầu. Cách giải quyết là viết một hàm tìm ước chung lớn nhất, chỉ cần tối giản các phân số $\dfrac{a}{b}$ và $\dfrac{c}{d}$ thì phương trình cũng sẽ được rút gọn.
  3. Trường hợp các nghiệm của phương trình là số nguyên luôn thì hiển thị như thế nào? Vậy là mình phải viết hàm hiển thị phân số, trong đó có xét tới trường hợp $x_1$ và $x_2$ là số nguyên.

Ngoài ra, ta còn xử lý kết quả hiển thị trong những trường hợp đặc biệt như hệ số bằng $\pm1$ hay bằng $0$…

Ý tưởng đã có, tiến hành thôi!

Thực hiện

Trước tiên, ta cần xây dựng 3 function như định hướng đã nêu.

//Random số ngẫu nhiên trong khoảng cho trước
function RandInt(min,max){
    return Math.floor(Math.random()*(max-min))+min;
}

//Tìm ước chung lớn nhất
function gcd(a, b) {
    return (b) ? gcd(b, a % b) : a;
}

//Hiển thị phân số numerator/denominator
function Fraction(num,den){
    var x = num/den;
    if (x == parseInt(x)) {
        return parseInt(x);
    } else {
        return "\\dfrac{"+num+"}{"+den+"}";
    }
}

Hàm RanInt và gcd, bây giờ ta random các biến $a,\,b,\,c,\,d$ đồng thời tối giản các biến này luôn.

a = RandInt(-9,9);
c = RandInt(-9,9);
b = RandInt(1,9);
d = RandInt(1,9);
//Tối giản các cặp a/b và c/d
a = a/Math.abs(gcd(a,b));
b = b/Math.abs(gcd(a,b));
c = c/Math.abs(gcd(c,d));
d = d/Math.abs(gcd(c,d));

Cuối cùng là hiển thị kết quả của phương trình bằng cách gán giá trị string cho biến $equation và replace các trường hợp đặc biệt. Để công thức toán học có thể hiển thị trên trình duyệt web, ta viết code theo chuẩn mã LaTeX và dùng thư viện Mathjax để render ra.

equation = "$"+(b*d)+"x^2+"+(-a*d-b*c)+"x+"+(a*c)+"=0\\Leftrightarrow\\left[\\begin{array}{l}x="+Fraction(a,b)+"\\\\ x="+Fraction(c,d)+".\\end{array}\\right.$";
//Replace các trường hợp đặc biệt
equation = equation.replace(/\+\-/g,"-").replace(/1x\^2/g,"x^2").replace(/\+1x/g,"+x").replace(/-1x/g,"-x").replace(/\+0x/g,"").replace(/\+0=0/g,"=0");
//In kết quả ra màn hình
document.write(equation+"<br>");

Chúng ta có thể dùng vòng lập for để in ra nhiều phương trình, ví dụ như sau:

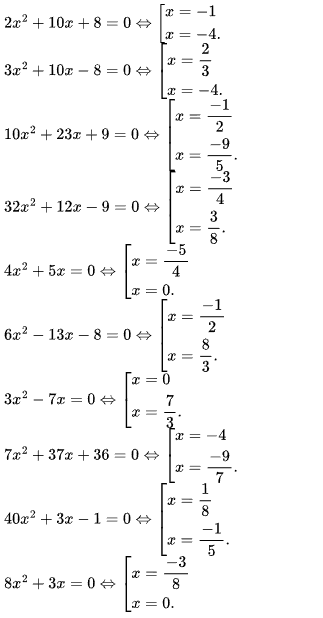
Sau đây là chương trình đầy đủ:

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>Document</title>
    <script src="https://polyfill.io/v3/polyfill.min.js?features=es6"></script>
    <script>
        MathJax = {
            tex: {inlineMath: [['$', '$'], ['\\(', '\\)']]},
            svg: {fontCache: 'global'}
        };
    </script>
    <script id="MathJax-script" async src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-svg.js"></script>
</head>
<body>
    <script>
        function RandInt(min,max){
            return Math.floor(Math.random()*(max-min))+min;
        }

        function gcd(a, b) {
            return (b) ? gcd(b, a % b) : a;
        }

        function Fraction(num,den){
            var x = num/den;
            if (x == parseInt(x)) {
                return parseInt(x);
            } else {
                return "\\dfrac{"+num+"}{"+den+"}";
            }
        }

        var a, b, c, d;
        var equation;

        for(var i=1;i<=10;i++){
            a = RandInt(-9,9);
            c = RandInt(-9,9);
            b = RandInt(1,9);
            d = RandInt(1,9);
            a = a/Math.abs(gcd(a,b));
            b = b/Math.abs(gcd(a,b));
            c = c/Math.abs(gcd(c,d));
            d = d/Math.abs(gcd(c,d));
            equation = "$"+(b*d)+"x^2+"+(-a*d-b*c)+"x+"+(a*c)+"=0\\Leftrightarrow\\left[\\begin{array}{l}x="+Fraction(a,b)+"\\\\ x="+Fraction(c,d)+".\\end{array}\\right.$";
            equation = equation.replace(/\+\-/g,"-").replace(/1x\^2/g,"x^2").replace(/\+1x/g,"+x").replace(/-1x/g,"-x").replace(/\+0x/g,"").replace(/\+0=0/g,"=0");
            document.write(equation+"<br>");
        }
    </script>
</body>
</html>

Mình chỉ vọc vạch nghiên cứu cho vui, ngờ đâu nó chạy được. Nay lưu lại để dành, sẳn chia sẻ cho anh em tham khảo, có gì không đúng, xin góp ý dưới phần bình luận để mình sửa ạ.

Bình luận

Chia sẻ
Thẻ: