Đề minh họa THPTQG 2019 có một câu đề cập đến diện tích của Elip, mà chương trình Hình học 10 cơ bản lại không có. Trong bài viết này, tôi sẽ dùng công cụ Tích phân trong Giải tích để tìm công thức tính diện tích Elip.
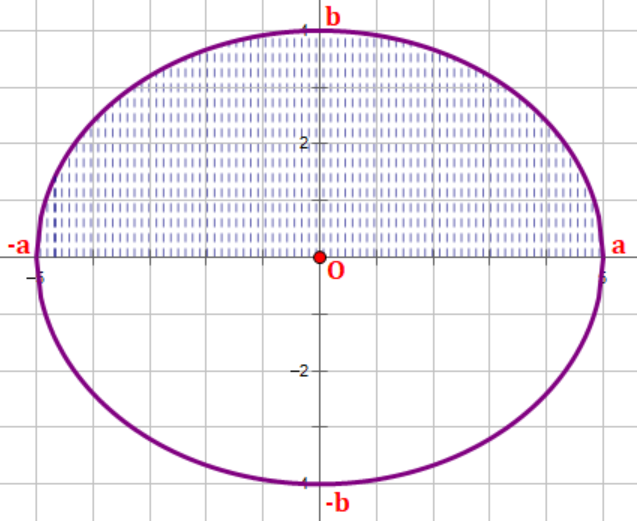
Giả sử elip $(E)$ có độ dài trục lớn là $2a$ và trục bé là $2b$. Khi đó
$$(E)\colon\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$$
Từ phương trình chính tắc này ta suy ra
$$y=\pm b\sqrt{1-\dfrac{x^2}{a^2}}$$
Vì $(E)$ có một phần nằm trên trục hoành và một phần nằm dưới trục hoành, hai phần này bằng nhau. Do đó, ta chỉ cần tính diện tích một phần, sau đó nhân đôi, tức là
$$S=2\int\limits_{-a}^{a}y\cdot dx=2\int\limits_{-a}^{a}b\sqrt{1-\dfrac{x^2}{a^2}}\cdot\mathrm{d}x$$
Đặt $x=a\sin t$ với $t\in\left[-\frac{\pi}{2};\frac{\pi}{2}\right]$.
$\Rightarrow\mathrm{d}x=a\cos t\cdot\mathrm{d}t$.
Đổi cận: $\begin{cases}x=a\Rightarrow t=\dfrac{\pi}{2}\\ x=-a\Rightarrow t=-\dfrac{\pi}{2}\\\end{cases}$
Khi đó
$$S=2b\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}\sqrt{1-\sin^2t}\cdot a\cos t\cdot dt=2ab\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}\cos^2t\cdot dt=\pi\cdot a\cdot b$$
Đặc biệt, nếu $a=b$, elip trở thành đường tròn, và $R=a=b$. Khi đó
$$S=\pi\cdot a^2=\pi\cdot R^2$$
Qua đây có thể thấy, không có ranh giới rạch ròi giữa các lĩnh vực Hình học, Đại số hay Giải tích. Chúng ta có thể dùng các công cụ và kiến thức thức của lĩnh vực này để lý giải và bổ sung cho lĩnh vực kia. Càng học nhiều thì càng thấy mình nhỏ bé.
