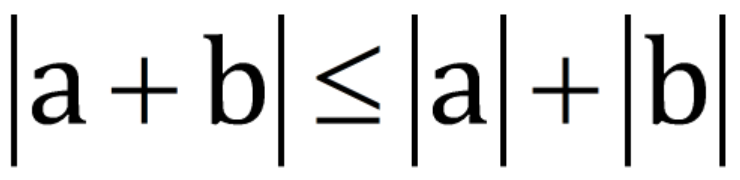
Khi nói về giá trị tuyệt đối, nhiều sách vở và tài liệu có nêu một tính chất rằng $|a+b|\leq|a|+|b|$, dấu “=” xảy ra khi $ab\geq0$. Vì sao lại thế?
Với mọi số thực $a, b$ ta đều có $ab\leq|a||b|$.
Dấu “=” chỉ xảy ra nếu $a$ và $b$ cùng dấu, tức là $ab\geq0$.
Nhân hai vế của bất đẳng thức cho $2$, sau đó cộng hai vế với $a^2+b^2$, ta được
$a^2+2ab+b^2\leq a^2+2|a||b|+b^2$
$\Leftrightarrow a^2+2ab+b^2\leq |a|^2+2|a||b|+|b|^2$
$\Leftrightarrow (a+b)^2\leq \left(|a|+|b|\right)^2$
Rút căn bậc 2 cả hai vế, ta được $|a+b|\leq|a|+|b|$.
Vì $|a|+|b|\geq0$, $\forall a, b$ nên $\sqrt{\left(|a|+|b|\right)^2}=|a|+|b|$, còn $a+b$ chưa biết âm hay dương nên $\sqrt{(a+b)^2}=|a+b|$.
Thì ra là thế!
