Tiêu đề bài viết chi mang tính trá hình, bịp bợm, vì thực chất là tôi sẽ vẽ tam giác nội tiếp elip thay vì vẽ elip ngoại tiếp tam giác. Mặc dù thành phẩm như nhau, nhưng cách làm thì lại khác biệt hoàn toàn, bạn đọc cân nhắc mục đích và hiệu quả trước khi áp dụng cách vẽ này nhe.
Ý tưởng chính của cách vẽ trong bài viết là tìm giao điểm của elip với bản sao của nó.
Bước 1. Vẽ elip
\draw[rotate=-20] (0, 0) ellipse (5 and 3);Tùy chọn [rotate=-20] có tác dụng xoay elip một góc $20^\circ$ theo chiều kim đồng hồ (chiều âm lượng giác), nếu muốn vẽ elip nằm ngang như bình thường, chúng ta chỉ cần xóa tùy chọn này đi.
Bước 2. Tạo ra bản sao và các giao điểm
\path[name path=elip1] (0, 0) ellipse (5 and 3);
\path[name path=elip2, rotate=-20] (0, 0) ellipse (5 and 3);
\path [name intersections={of = elip1 and elip2}];
\coordinate (D) at (intersection-1);
\coordinate (A) at (intersection-2);
\coordinate (B) at (intersection-3);
\coordinate (C) at (intersection-4);Phần này sẽ không hiện kết quả ra màn hình, do đó, muốn biết giữa hai elip cắt nhau tại bao nhiêu điểm và vị trí các điểm có thỏa mãn yêu cầu hay chưa, chúng ta có thể thử nghiệm bằng cách test thử bằng đoạn code sau:
\begin{tikzpicture}[line join=round, line cap=round, >=stealth]
\draw[dashed] (0, 0) ellipse (5 and 3);
\draw[rotate=-20] (0, 0) ellipse (5 and 3);
\path[name path=elip1] (0, 0) ellipse (5 and 3);
\path[name path=elip2, rotate=-20] (0, 0) ellipse (5 and 3);
\path [name intersections={of = elip1 and elip2}];
\coordinate (D) at (intersection-1);
\coordinate (A) at (intersection-2);
\coordinate (B) at (intersection-3);
\coordinate (C) at (intersection-4);
\foreach \x/\g in {A/180,B/-90,C/0,D/90}
\draw[fill=white] (\x) circle (1.5pt)+(\g:3mm) node {$\x$};
\end{tikzpicture}Kết quả ta nhận được như sau:
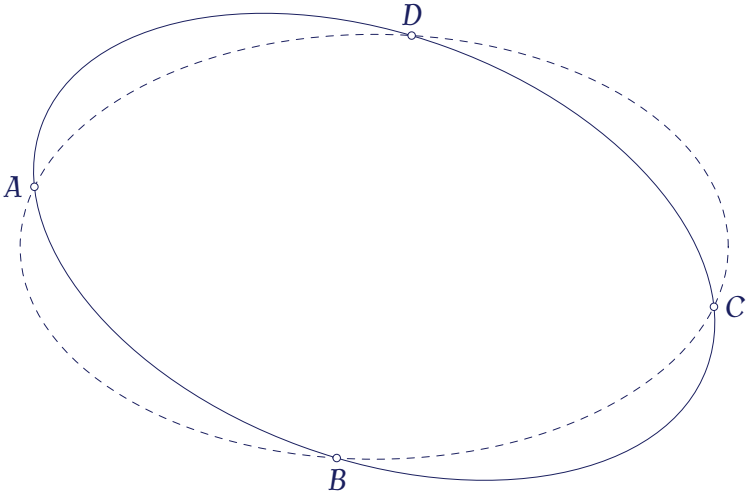
Sau khi cảm thấy hài lòng, ta ẩn đi những đoạn mã không cần thiết, sau đây là đoạn code hoàn chỉnh:
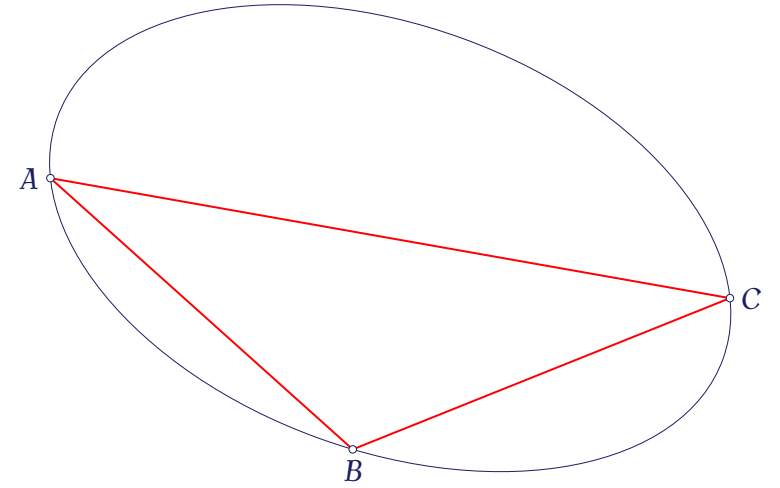
\begin{tikzpicture}[line join=round, line cap=round, >=stealth]
%\draw[dashed] (0, 0) ellipse (5 and 3);
\draw[rotate=-20] (0, 0) ellipse (5 and 3);
\path[name path=elip1] (0, 0) ellipse (5 and 3);
\path[name path=elip2, rotate=-20] (0, 0) ellipse (5 and 3);
\path [name intersections={of = elip1 and elip2}];
\coordinate (D) at (intersection-1);
\coordinate (A) at (intersection-2);
\coordinate (B) at (intersection-3);
\coordinate (C) at (intersection-4);
\draw[thick,red] (A)--(B)--(C)--cycle;
\foreach \x/\g in {A/180,B/-90,C/0}
\draw[fill=white] (\x) circle (1.5pt)+(\g:3mm) node {$\x$};
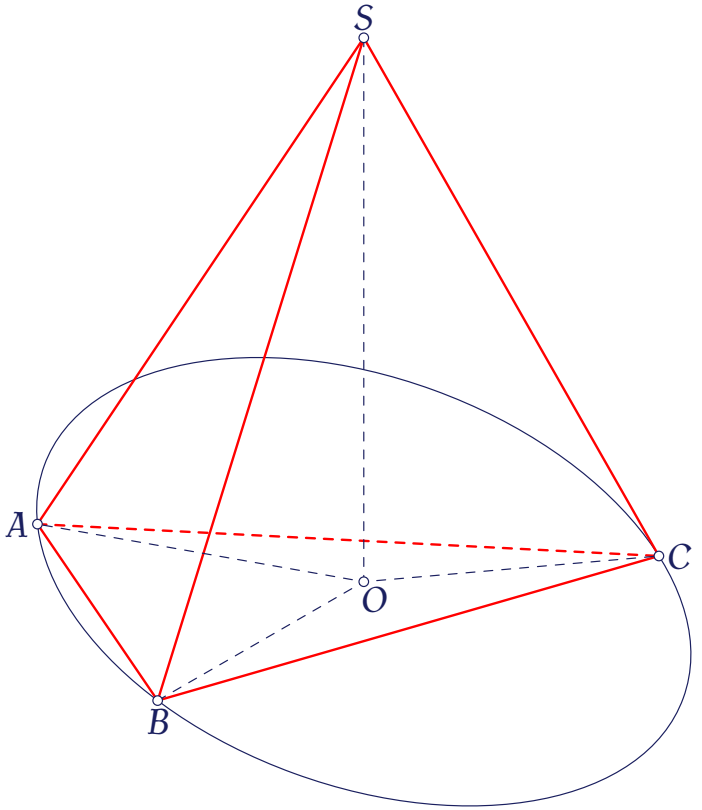
\end{tikzpicture}Cuối cùng, mục đích chính của tôi khi nghiên cứu vấn đề này là vẽ một hình chóp tam giác có các cạnh bên bằng nhau (hay góc hợp bởi các cạnh bên với mặt đáy bằng nhau). Ngoài ra, vị trí các điểm A, B, C như trên không được như tôi mong đợi, thậm chí có hai điểm đối xứng nhau qua tâm của elip. Vậy nên tôi phải phức tạp hóa code này.
\begin{tikzpicture}[line join=round, line cap=round, >=stealth,scale=0.8]
\draw[rotate=-20] (0, 0) ellipse (5 and 3);
\path[name path=elip1] (0, 0) ellipse (5 and 3);
\path[name path=elip2, rotate=-20] (0, 0) ellipse (5 and 3);
\path[name path=elip3, rotate=30] (0, 0) ellipse (5 and 3);
\path[name path=elip4, rotate=80] (0, 0) ellipse (5 and 3);
\path [name intersections={of = elip2 and elip1}];
\coordinate (A) at (intersection-3);
\path [name intersections={of = elip2 and elip3}];
\coordinate (C) at (intersection-1);
\path [name intersections={of = elip2 and elip4}];
\coordinate (B) at (intersection-3);
\coordinate (S) at (0,8);
\coordinate (O) at (0,0);
\draw[thick,red] (S)--(B)--(A)--(S)--(C)--(B);
\draw[thick,red,dashed] (A)--(C);
\draw[dashed] (S)--(O)--(A) (B)--(O)--(C);
\foreach \x/\g in {A/180,B/-90,C/0,S/90,O/-60}
\draw[fill=white] (\x) circle (2pt)+(\g:3mm) node {$\x$};
\end{tikzpicture}Và đây là thành quả: