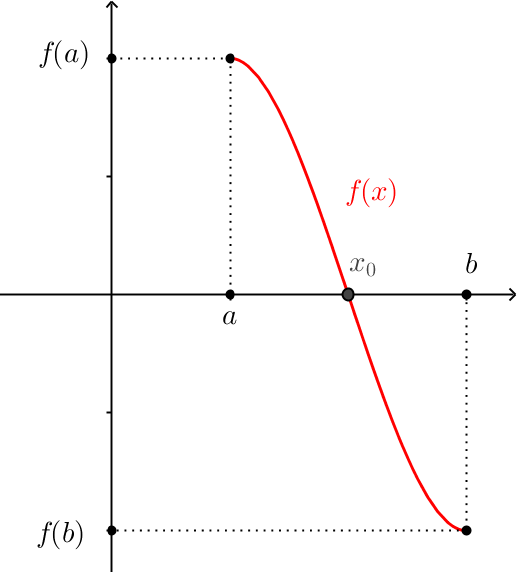
Ứng dụng hàm số liên tục tìm nghiệm vô tỉ của phương trình

Trong chương trình Giải Tích 11 có một định lý hết sức thú vị, liên quan đến nghiệm của phương trình. Định lý như sau:

Nếu hàm số $f(x)$ liên tục trên đoạn $[a;b]$ và $f(a)\cdot f(b)<0$ thì phương trình $f(x)=0$ có ít nhất một nghiệm $x_0\in(a;b)$.

Bây giờ, tôi sẽ thử ứng dụng định lý này để tìm tòi một nghiệm vô tỷ của phương trình $x^2-2^x=0$.

Xét hàm số $f(x)=x^2-2^x$. Hàm số này xác định trên $\mathbb{R}$ và có đồ thị như sau:

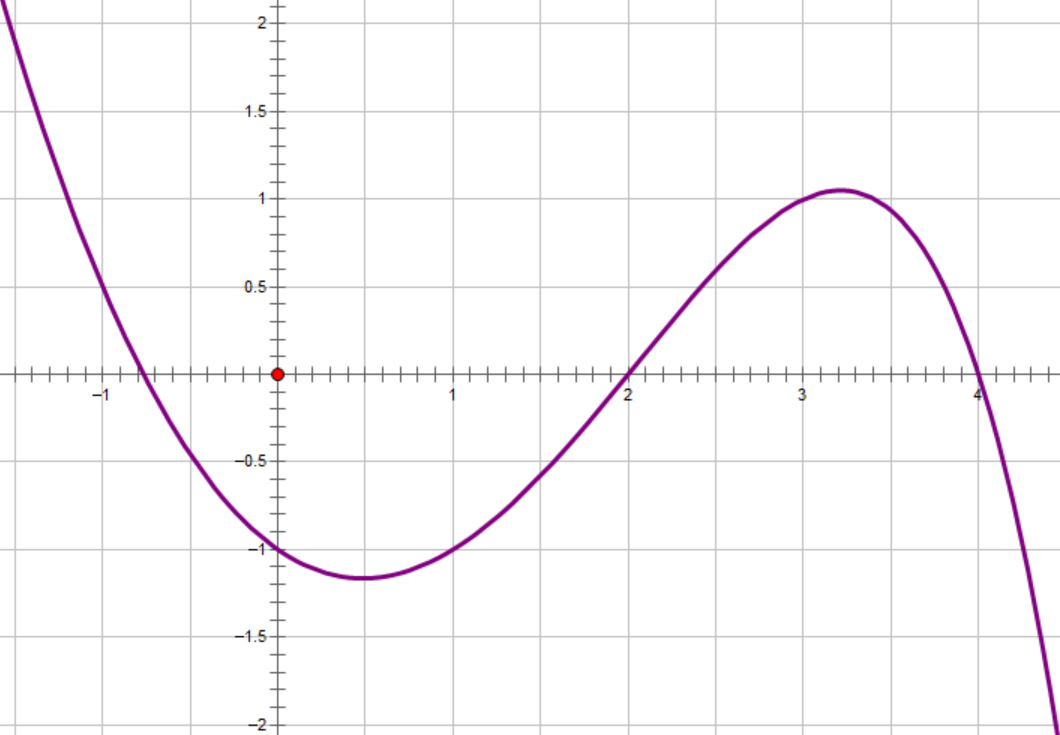
Dễ thấy, đồ thị cắt trục hoành tại $3$ điểm phân biệt là $x_1=2$, $x_2=4$ và $x_3$ là một số âm nằm trên đoạn $[-1;0]$. Rõ ràng, đây không phải nghiệm nguyên, thậm chí nó còn chưa chắc là nghiệm hữu tỷ nữa.

Ý tưởng của việc tìm nghiệm này như sau:

  • Bước 1: Vì $f(-1)\cdot f(0)=0.5\cdot(-1)=-0.5<0$ nên chắc chắn có một nghiệm $x_3\in[-1;0]$.
  • Bước 2: Chia đoạn $[-1;0]$ thành hai đoạn bằng nhau là $[-1;-0.5]$ và $[-0.5;0]$.
    Nếu $f(-1)\cdot f(-0.5)<0$ thì chắc chắn $x_3\in[-1;-0.5]$, ngược lại, $x_3\in[-0.5;0]$.

Lặp đi lặp lại Bước 2 cho tới khi khoảng cách hai đầu mút của đoạn đủ nhỏ, khi đó giá trị trung bình của đoạn có thể xem như là là giá trị gần đúng của nghiệm cần tìm.

Việc này không thể làm thủ công được, nên tôi sẽ dùng công nghệ thông tin hỗ trợ tôi việc này. Cụ thể, tôi sẽ viết một file PHP, trong đó sẽ có:

  1. Một function HamSo(\$x) để tính giá trị của $f(x)$.
  2. Một function Nghiem(\$a, \$b) để xử lý đoạn $[a;b]$. Hàm này là hàm đệ quy, sẽ lặp theo điều kiện cho trước, ở đây tôi đặt điều kiện là “độ chính xác 1/10 tỷ”.
<?
    function HamSo($x){
        return pow($x,2)-pow(2,$x);
    }
    function Nghiem($a, $b){
        $c=round(($a+$b)/2,12);
        $d=$b-$a;
        echo "<br>".$a." : ".$c." : ".$d."<br>";
        if($d>1/10000000000){
            $x=HamSo($a);
            $y=HamSo($c);
            $z=HamSo($b);
            if($x*$y<0){
                Nghiem($a, $c);
            }else{
                Nghiem($c, $b);
            }
        }else{
            echo $c;
        }
    }

    Nghiem(-1,0);
?>

Vì để quan sát quá trình chia đoạn của chương trình được thực hiện ra sao, tôi đã thêm dòng  echo “<br>”.\$a.” : “.\$c.” : “.$d.”<br>”;  để nó hiển thị kết quả của từng bước chia ra màn hình.

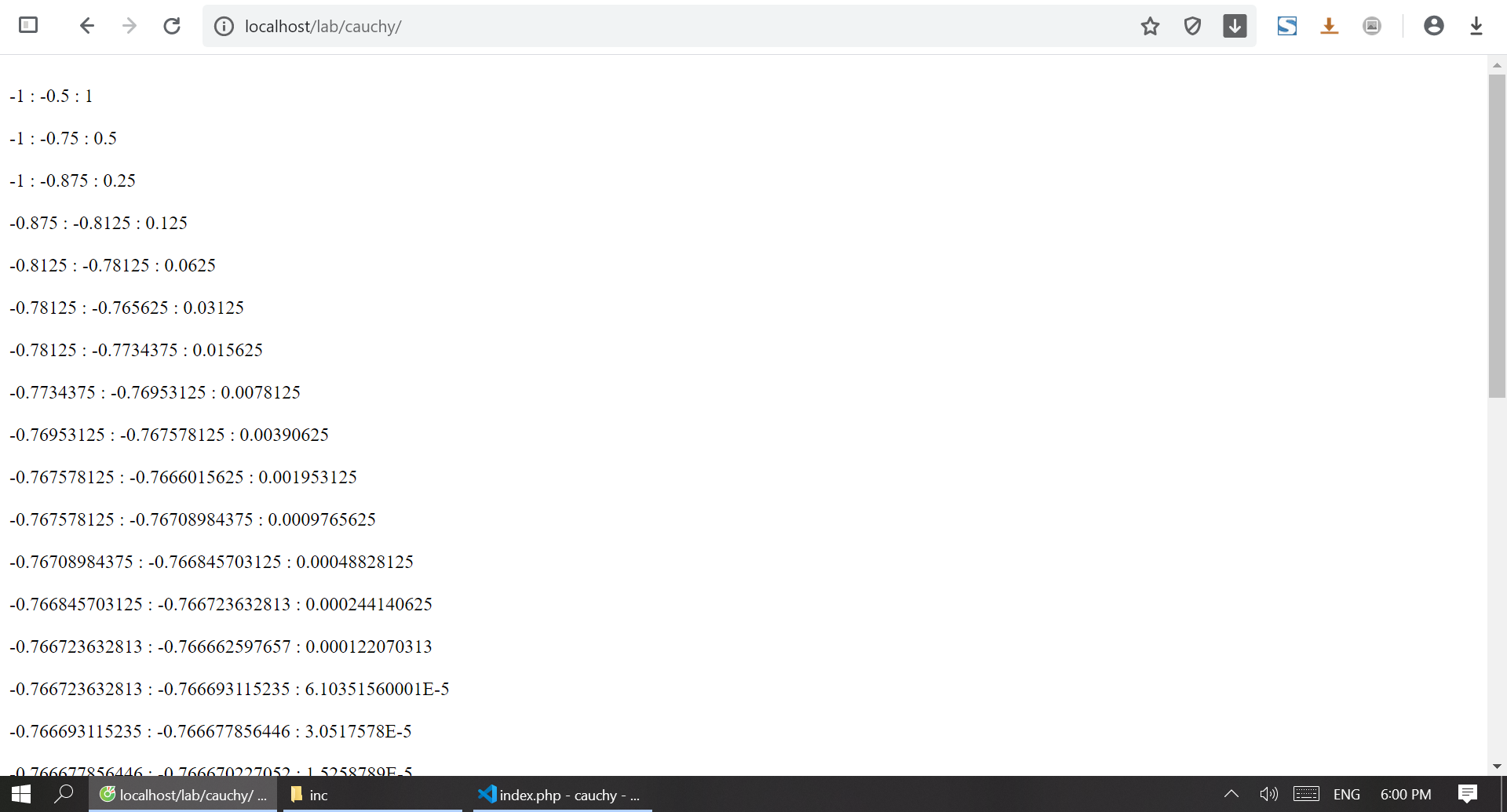
Và kết quả thu được sau khi chương trình kết thúc là một số thập phân vô hạn không tuần hoàn $-0.766664695958$.

Mặc dù PHP chỉ là ngôn ngữ backend của web nhưng thông qua thực nghiệm này cũng đủ thấy nó thực sự mạnh mẽ như thế nào. Sắp tới, tôi sẽ làm thêm mốt số ví dụ về xác suất, mời mọi người đón xem.

Bình luận

Chia sẻ
Thẻ: