Lựa chọn bài toán thích hợp cho từng đối tượng học sinh và phân bậc hoạt động là một trong những việc hết sức quan trọng trong việc rèn luyện kỹ năng giải toán cho học sinh. Nếu thực hiện hợp lý, chẳng những có thể kích thích tinh thần và hứng thú làm bài của học sinh mà còn mang lại hiệu quả cao trong công tác giảng dạy.
Thông thường, đại đa số giáo viên đều đánh giá mức độ khó của một bài toán chủ yếu là cảm tính, chủ quan, duy ý chí. Tui thấy nó dễ, thì tức là nó dễ. Tuy nhiên, ở góc nhìn của học sinh thì điều này là chưa chắc. Vậy, thước đo nào để đánh giá được chính xác (hoặc tương đối chính xác) mức độ dễ – khó của một bài toán?
Câu trả lời là, phải dựa vào các số liệu cụ thể và minh chứng rõ ràng. Thông qua việc trắc nghiệm khách quan trên quy mô lớn, áp dụng cho mọi đối tượng học sinh, thì số liệu thu về sẽ cho ta biết mức độ dễ – khó của một bài toán.
Nhận diện mức độ khó của câu hỏi thông qua số liệu thống kê
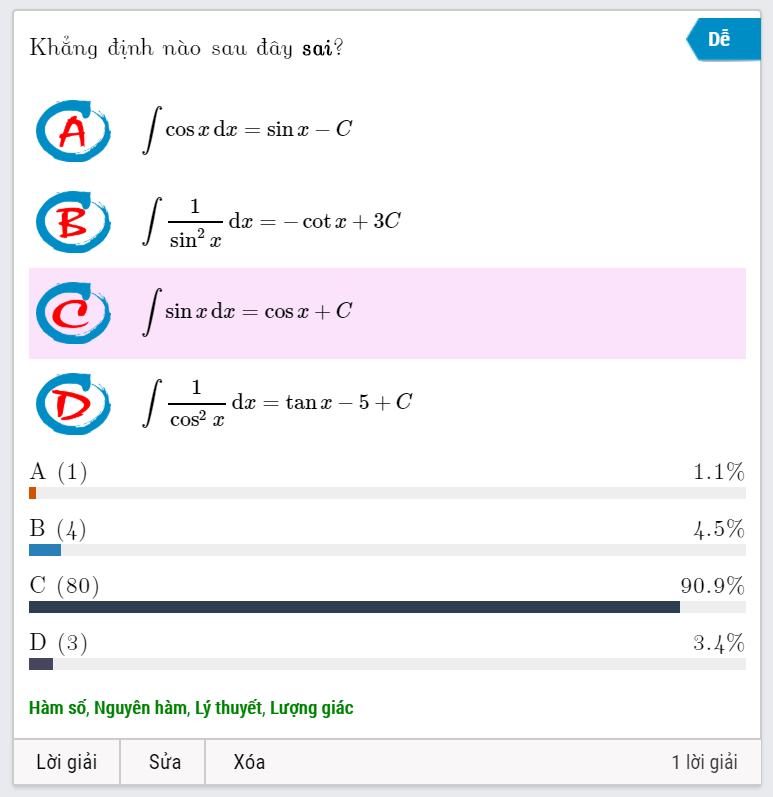
- Mức độ dễ: Các câu hỏi mức độ này thì học sinh rất dễ nhìn ra đáp án đúng, vì ít đánh đố, nhận biết và thông hiểu lý thuyết chiếm phần nhiều, hoặc là áp dụng công thức mức độ thấp. Do đó, tỉ lệ chọn đúng đáp án rất cao.

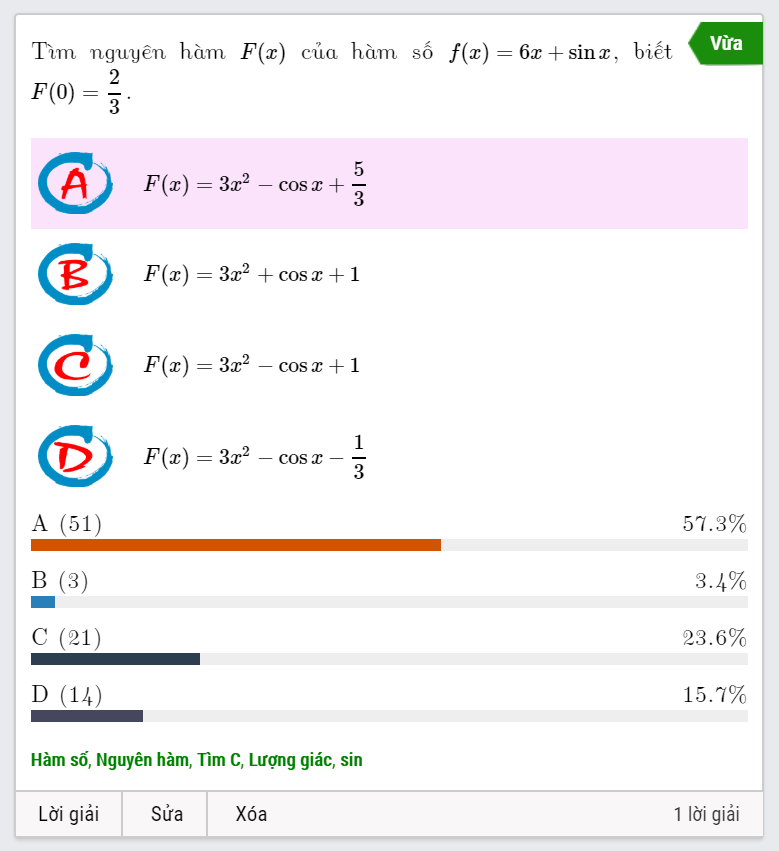
- Mức độ vừa: Các câu hỏi mức độ này thường dành cho học sinh cấp trung bình và khá, đòi hỏi học sinh có sự hiểu biết sâu hơn về lý thuyết, vận dụng được cho nhiều trường hợp với mức độ cao hơn. Tỉ lệ chọn phương án đúng ở các câu hỏi này vẫn cao, song, tỉ lệ chọn các phương án sai cũng tương đối cao do có sự đánh đố hoặc do sơ suất, tính toán sai lầm…
- Mức độ khó: Các câu hỏi mức độ này đòi hỏi học sinh có sự hiểu biết sâu sắc hơn, biết vận dụng nhiều kỹ năng, liên hệ rất nhiều kiến thức đã học (thậm chí không có trong sách giáo khoa), biết dựng hình, phân tích bài toán thực tế – liên môn… Nhiều câu hỏi trời ơi đất hỡi, hạn chế bấm máy và đánh đố rất cao, do đó khả năng chọn sai đối với các câu hỏi này là rất lớn. Học sinh có khuynh hướng chọn đại rất cao đối với các câu hỏi mức độ này.

Ghi chú: hình ảnh này chỉ mang tính chất minh họa, vì số liệu quá ít, không đủ minh chứng.
Một số lưu ý trong quá trình đánh giá
Thứ nhất, để việc đánh giá mức độ khó của một bài toán thì số liệu thống kê phải nhiều, tối thiểu là vài trăm, thậm chí vài nghìn. Nếu chỉ dựa trên thiểu số mà đánh giá cho đa số thì đó là chủ quan, duy ý chí, uổng phí công sức làm thống kê.

Thứ hai, trong quá trình thống kê, nếu nhận thấy phương án nhiễu nào có tỉ lệ chọn nào quá thấp, thậm chí không có lượt chọn nào, thì đó là một phương án nhiễu quá tồi, cần phải cách ly và thay thế ngay. Nếu đã dùng câu hỏi trắc nghiệm thay thế cho câu hỏi tự luận để đánh giá năng lực của học sinh, thì các phương án nhiễu phải đảm bảo tính khách quan. Tùy vào mức độ khó của câu hỏi mà phương án nhiễu cũng phải linh hoạt theo. Một phương án nhiễu mà học sinh không thèm liếc mắt một cái thì một là đề bài chưa hợp lý, hai là đề bài không hề hợp lý.
Kết luận
Hiện nay, trong công tác dạy học vẫn còn nhiều bất cập, chủ yếu đến từ sự chủ quan, duy ý chí của người dạy. Cái khó là chưa có các số liệu thống kê để đánh giá các vấn đề một cách chính xác, khách quan, để từ đó mỗi người sẽ đưa ra cách thức thực hiện thích hợp nhất cho chuyên môn, cho học sinh của mình, nhằm đạt được kết quả cao nhất. Khó hơn nữa chính là cách thức làm sao để thu được các số liệu này. Nếu chỉ thống kê bằng tay thì mỗi giáo viên, mỗi nhà giáo dục sẽ phải đánh đổi bằng rất nhiều thời gian, công sức và tiền bạc. Chỉ có công nghệ với cuộc cách mạng 4.0 mới có thể hiện thực hóa việc này.
Ứng dụng Toán Học Tiểu Toàn Thư không chỉ là một ứng dụng học tập Toán hiệu quả cho học sinh mà còn là một giải pháp tối ưu để giáo viên có thể đánh giá được rất nhiều vấn đề trong chuyên môn. Khi dữ liệu đủ lớn, đủ tối ưu, tôi dự định sẽ hợp tác với một số đồng nghiệp tâm huyết khác để xây dựng giải pháp chung cho việc giảng dạy môn Toán nói riêng và trong ngành giáo dục nói chung. Toán Học Tiểu Toàn Thư một khi đã hoàn thiện thì cũng là lúc mô hình này được nhân rộng cho các môn khác nữa.
Trong các bài viết sau, tôi sẽ lần lượt trình bày các thực nghiệm khác dựa trên ứng dụng Toán Học Tiểu Toàn Thư. Xin chào và hẹn gặp lại!
